|
|
| FORMULARIO DEL ÁTOMO |
|
ÁTOMO |
||
|
PRIMEROS MODELOS |
||
| Notación isotónica |
A X Z |
X : símbolo del elemento Z : número atómico A : número másico |
| Mezclas isotópicas |
∑ Ai · xi A = ————— 100 |
A : masa atómica del elemento natural Ai : masa atómica de cada isotopo xi : porcentaje de cada isótopo en la mezcla |
| Ecuación de Einstein |
∆E = ∆m ·
c2
∆E = ∆m · 931,2 (MeV) (∆m en uma) |
∆E : Energía convertida ∆m : masa convertida c : velocidad de la luz (vacio=3·108 m/s) uma : unidad de masa atómica |
| Defecto de masa | ∆m = Z · mprotón + (A-Z) · mneutrón - M | M : masa del nucleo |
| Energía de ligadura por nucleón | En = ∆E / A | |
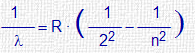
|
n : número entero λ : longitud de onda de cada raya de la serie. (1/λ) : núnero de onda R : cte de Rydberg = 109 740 cm-1 |
|
| Primer postulado de Bohr | El electrón describe órbitas circulares alrededor del nucleo sin emitir energía (estacionario) | |
| Segundo postulado de Bohr | L = I · w = m · v · r = n ·h / (2π) |
L: momento angular I=mr2 (momento de inercia del electrón que gira alrededor del nucleo). w : velocidad angular (v/r). r : radio de la órbita del electrón h = 6,63·10-34 (cte de Plank) v : velocidad lineal del electrón |
| Tercer postulado de Bohr | Ei - Ef = h · n = h · c / λ |
Ei : energía del electrón en la óbita estacionaria inicial Ef : energía del electrón en la óbita estacionaria final n : frecuencia de la radiación λ : longitud de onda de la radiación |
| Energía total del electrón en una órbita estacionaria | E = - k·e2 / (2·r) |
e : carga del electrón r : radio de la órbita k : 9·109 |
| Radio de una órbita estacionaría |
h2 r = —————— · n2 = 0,529 · n2 (Å) 4π2·m·e2 |
n : número cuántico principal m : masa del electrón |
| Longitud de onda de las rayas espectrales |
 |
K>J J=1 K=2,3,.. serie Lyman J=2 K=3,4,.. serie Balmer J=3 K=4,5,.. serie Paschen J=4 K=5,6,.. serie Brackett J=5 K=6,7,.. serie Pfund |
| Ampliación para iones hidrogenoides |
 |
Z : carga nuclear del ion |
|
Espectro de rayos X Ley de Monseley |
1
—— = K · ( Z - s)2 λ |
K y s son ctes distintas para cada raya |
|
MODELO ACTUAL |
||
|
Energía Radiante (M. Plank) |
E = h · ν | h : cte de Plank (6,63·10-34) |
|
Efecto fotoelétrico
|
Wo = h · νo ; h · ν - Wo = m·v2/2 |
Wo : potencial de extracción νo : frecuencia umbral |
| Efecto Compton |
|
m : masa en reposo del electrón c : velocidad de la luz (vacio) φ : ángulo de dispersión λ, λ' : longitud de onda del fotón incidente y dispersado |
| Corrimiento de Compton |
h ———— = 2,43 · 10-12 m = 0,0243 Å m · c |
|
|
Hipótesis de De Broglie
|
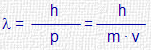 |
m : masa en movimiento de la partícula v : velocidad de la partícula p : momento lineal de la partícula λ : longitud de onda asociada |
|
Principio de incertidumbre de
Heisenberg
|
∆x · ∆px ≥ h |
∆x : incertidumbre en la medida de la posición de la partícula. ∆px : incertidumbre en la medida del momento lineal de la partícula. |
|
Valores de los cuatro números
cuánticos
|
n : 1, 2, 3, 4, ... (K, L, M, N, ...) l : 0, 1, 2, ... (n-1) (s, p, d, f) m : -l, ... ,0, ... +l s : ± ½ |
n : número cuántico principal l : número cuántico secundario m : número cuántico magnético s : número cuántico de spin |
|
|